The year was 1974 dating back fifty years. The venue was Kandy – St. Anthony’s College to be specific. As a young teacher, I ventured to form a mathematics laboratory, the first of its kind in Sri Lanka, with the idea of changing the perception of students that mathematics is a challenging subject that can be learnt only by those who are naturally gifted with numbers.

First, let me explain the purpose of a Maths Lab. The primary objective of a maths lab is to create a location consisting of mathematical apparatus and visual aids to enable students to involve themselves in the learning process, by attempting to bridge the gap between the real world and the abstract world. It provides opportunities for students to develop inquiry-based learning in a mathematical atmosphere, thereby enhancing their interest in the subject and confidence to face the challenges that it offers. All students move through a development sequence from concrete to abstract when learning mathematics and a maths lab is an excellent idea to help them through this process.

I took these ideas to the then Principal of the school, the late Fr. Aiden de Silva and had a discussion as it required the reservation of a room and also the involvement of the school carpenter. With his full blessings and unmitigated support, I embarked on this memorable journey which involved a tremendous amount of labor, time and effort. An excellent set of students not only helped but also inspired me in the formation of the lab, where all models, equipment and apparatus were our own products as these were not available to be purchased at that time. The school carpenter did an excellent job with the wooden models with their production according to the exact measurements given to him by me in the form of a design on paper. All paper models were done by the students with my guidance.

I was a member of the library of USIS (United States Information Center) in Kandy and I remember borrowing the book titled ‘Mathematical Models’ by Cundy & Rollett, which is an excellent resource for mathematical apparatus for secondary students. It could be borrowed only for a period of two weeks. After returning the book, I went to the library leaving a gap of a day to borrow it again as there were no photocopiers at that time. Most of the ideas came through this great resource.

We decided to have suitable wall display items to establish and enhance the mathematical atmosphere of the room. The students and teachers who had artistic talents helped me to draw sketches of great mathematicians and write brief descriptions of their contributions with the idea of the creation of an awareness and appreciation of the history of mathematics. Examples were Pythagoras (380 – 300 BC) whose work contributed towards the growth of the number system, Archimedes (287 – 212 BC) who worked on spatial concepts contributing towards the foundations of geometry and mechanics, Descartes (1596-1650) who gave us analytic geometry combining algebra and geometry, Isaac Newton (1643-1727) who changed the whole format of mathematics through calculus and Einstein (1879-1955) who gifted us with the theory of relativity. We also included displays of optical illusions and tessellations to show the power of imagination.

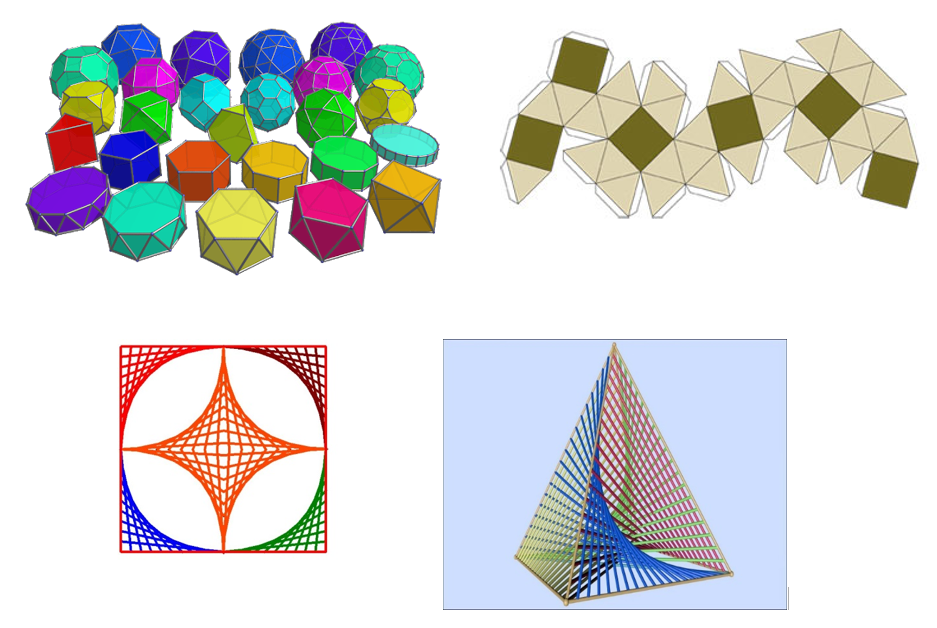
Most paper models such as polyhedral solids were made by the students themselves. It was hard work as they had to first draw the nets according to exact measurements and thereafter fold them properly and paste the flaps to obtain the solids. The polyhedron models provide a good idea about the three-dimensional shapes and their formation. We also prepared Napier rods in the form of boxes. These can get students accustomed to different methods of multiplication. Magic squares were also made to develop interest in numbers and their properties.

Creative display items are important for the students to maintain an interest in creativity and get them enthusiastic about the search for pattern, which is an important aspect of mathematics. One example is the formation of envelops through curve stitching, to show how different curves can be visually obtained using straight lines. Our students did this beautifully using boards, nails or pins and strings to come up with impressive designs. One such display item was the words ‘MATHS LAB’ done with such strings. We even extended it to a three-dimensional shape to form a hyperboloid with strings.

The wooden models were done with the help of the school carpenter. Some of the items that were made are listed below.

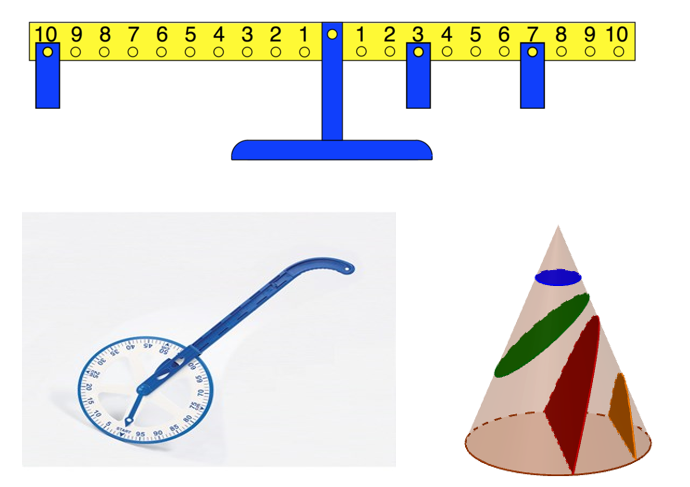
• A mathematical balance to reinforce the idea of solving equations.
• A nomogram to help students to deal with negative numbers.
• A trundle wheel to measure curved distances.
• A conic section model to visualize the formation of shapes such as parabola, ellipse and hyperbola.
• An experimental model of a cycloid path to verify the path of the shortest possible time.
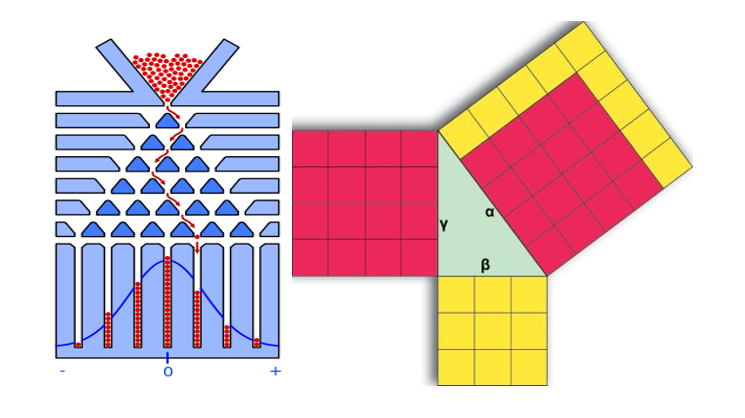
• An experimental probability model to relate with the Pascal’s triangle and the normal curve.
• A model of a unit circle to obtain the values of the three trigonometric ratios and show the properties of the four quadrants.
• Hinged rods to verify the basic geometric theorems.
• Foldable triangle to show that the sum of angles is 360⁰.
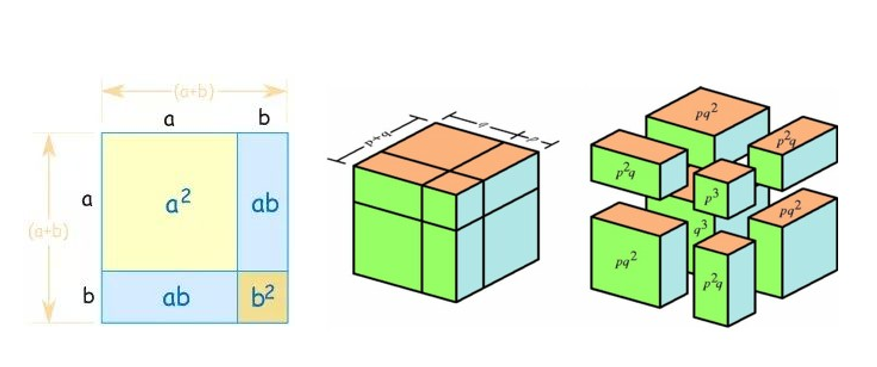
• An assembling model to show how the Pythagoras’ Theorem works
• An experimental model to approximate the value of Pi.
• Reuleaux triangle to show the application of non-circular wheels.

The pictures of some of these models are shown alongside this article as examples. The creation of these models often led to inquiries from my students which demonstrated imagination and innovation. I remember one such incident clearly. We had a wooden model to show the result obtained when (a + b)² is expanded. A student debated that if it could be done for a square, then we could use the same idea to obtain the expansion of (a + b)³. Thereafter, we created another model which when dissembled gave us the correct result. A good maths lab will promote and encourage mathematical exploration. Mathematics learning could be made fun and productive through the effective use of a mathematics laboratory. A Chinese proverb states “I hear, and I forget; I see, and I remember; I do, and I understand”.

It was a memorable and highly rewarding project although I may have had sacrificed many of my sleeping hours for planning and designing. Many students and teachers from all parts of the country visited the maths lab and offered praise and encouragement. In 1979, Rev. Fr. Stephen Abraham took over the reigns as the principal and with his unwavering and ardent support the maths lab was further developed and strengthened. In the same year, the school celebrated its 125^th anniversary with a grand educational exhibition and the maths lab was the star attraction. In 1981, I left the school to complete the post-graduate education and later left the country to take up a posting in Hong Kong. When I returned after retirement and visited the school, I could not find a single item that we painstakingly created. Instead, there was a modernized maths lab. As Heraclitus said “there is nothing permanent except change”.

A good number of students who were involved in the formation of this maths lab are still in touch with me and their love for mathematics is still noticeable. I have dedicated my recent book titled ‘Mathematics in action’ in honor of them.

R N A de Silva

rnades@gmail.com

The author is an educational consultant at The Overseas School of Colombo and a senior examiner of the International Baccalaureate Organization, UK.